Проблемы численных методов решения нелинейных алгебраических уравнений. Гибридные алгоритмы.

Содержание:

  1. Введение
  2. Итерационные методы решения нелинейных уравнеий
    1. Локализация корня
    2. Итерационное уточнение корня
  3. Гибридные методы

Введение

Одним из важнейших критериев, характеризующий любой метод решения какой-либо задачи, является его универсальность. Человеку свойственно творческое мышление, поэтому он способен, анализируя сложившуюся ситуацию, нетривиально подходить к решению той или иной проблемы. То есть, если задача специфична и не сочетается ни с одним из известных методов ее решения, человек посредством своего уникального мышления, внеся ряд поправок в метод, может получить устраивающий его результат.

К чему это было сказано? А к тому, что электронно-вычислительная машина «не умеет творчески мыслить», она лишь выполняет последовательность команд, образующих алгоритм. А хороший алгоритм – это такой алгоритм, у которого спектр решаемых задач больше.

Целью этой статьи не является подробное описание численных методов решения нелинейных уравнений. Я лишь мельком пробегусь по некоторым из них, остановив внимание на самом механизме метода, и вследствие этого выявлю достоинства и недостатки.

Итерационные методы решения нелинейных уравнений

В большинстве случаев курс вычислительной математики начинают как раз с изучения методов решения нелинейных уравнений. Это оправдано тем, что материал в действительности достаточно прост. Но чем тогда объяснить те сложности, с которыми сталкиваются студенты при реализации этих методов в своих программах? Дело в том, что процесс решения нелинейного уравнения f(x)=0 имеет множество малозначимых на первый взгляд нюансов. Эти нюансы, например выбор начальных приближений к корню уравнения, зависят от вида f(x) и от метода решения. Я расскажу, как правильно выбирать начальные приближения, но об этом чуть позже.

А теперь по порядку. Процесс решения нелинейного уравнения разделен на две стадии:

  1. Локализация корня;
  2. Итерационное уточнение корня.

Локализация корня

Первый этап заключается в том, что производится поиск всех подынтервалов [x;x+h] (h-шаг сетки), на которых локализованы по одному корни уравнения. Для выполнения этой задачи наиболее удобен, в силу своей простой программной реализации, графический метод или, по-другому, метод сканирования. Суть метода состоит в том, что искомый участок оси абсцисс [a;b] делится на подынтервалы, длина которых равна h. Каждый из этих подынтервалов подвергается проверке на выполнение следующего условия: f(x)*f(x+h)<0. Из положительного результата проверки следует, что на исследуемом подынтервале локализовано нечетное количество корней. Отрицательный исход говорит нам о четном числе решений. Следовательно, метод сканирования не дает нам 100-процентной гарантии получения верных данных на этапе локализации. Да, аналитически мы можем исследовать и первую и вторую производную функции f(x) и в итоге получить максимально точное ее поведение. Может и возможно как-нибудь «впихнуть» эту аналитику в программный код, но по ряду причин это совершенно нецелесообразно. Проще взять величину шага h поменьше и, в результате, свести к минимуму вероятность фиксирования интервалов с числом корней отличным от одного. У метода сканирования существует и еще одна проблема. Дело в том, что таким способом исключена возможность локализации кратных корней, то есть таких, где функция только касается оси абсцисс и, следовательно, знак в своей окрестности не меняет (например f(x)=x2) . Также хочу отметить, что в программе лучше записывать условие локализации в виде f(x)*f(x+h)<=0, дабы исключить возможность потери решений.

Итерационное уточнение корня

После того как корни локализованы применяют один из методов решения нелинейных уравнений. Все они итерационные. Это значит, что задействуется итерационный процесс, на каждой итерации которого, то есть совокупности повторяющихся команд, происходит постепенное приближение к корню вплоть до того момента, когда полученный результат удовлетворит требуемой точности Ɛ. Я ограничусь четырьмя методами: бисекции, простой итерации, касательных (метод Ньютона) и секущих (одна из модификаций метода Ньютона).

Механизм метода бисекции, который больше известен под названием метода половинного деления, очень прост и заключается в том, что полученный при локализации отрезок на каждой итерации делится пополам. Из двух половинок выбирается та, на концах которой функция принимает значения противоположных знаков. То есть проверяется то же условие, что и при методе сканирования. Процесс заканчивается, когда длина полученного интервала становится меньше произведения 2Ɛ. Фактически этот метод исключает возможность появления ошибки. «Аварийная» ситуация может быть вызвана лишь тем, что граница полученного на итерации отрезка попадет в точку разрыва функции. Метод половинного деления наиболее универсальный среди всех итерационных методов. Но, как всегда, бочка меда не обходится без ложки дегтя – для бисекции характерна очень низкая скорость сходимости.

Итерационная формула метода бисекции:


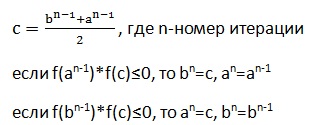
Скорость сходимости: низкая

Надежность сходимости: высокая

В самом начале статьи я говорил, что хорошим методом можно считать универсальный метод. Так вот, метод простой итерации и универсальность, по моему мнению, совершенно несовместимые понятия. Изначально я вообще считал, что данный метод – это всего-навсего общее наименование всех методов решения нелинейных уравнений.

Фактически все способы решения НАУ различаются между собой механизмом. Механизм определяется итерационной формулой. То есть итерационная формула это и есть отличительная черта каждого метода. А в методе простой итерации этой формулы нет. Вернее эту формулу должен определить сам разработчик. Она имеет общий вид xn=ϕ(xn-1).Причем чтобы итерационный процесс сходился, должно выполняться условие: |ϕ’(x)|<1 в каждой точке интервала локализации. Да, разработчику не составит большого труда вычислить итерационную формулу для одного отрезка локализации. Но если ему нужно, например, решить кубическое уравнение и обеспечить нахождение любого из трех корней (куб. ур-ие максимально имеет три решения)? В этом случае методом простых итераций он не достигнет цели, так как итерационная формула не может гарантировать одинаково хорошего результата на нескольких диапазонах, хватит лишь того, что исходная функция на одном интервале будет убывать, а на другом возрастать.

Вот этим и объясняется «неуниверсальность» метода простых итераций. Этот способ скорее имеет какой-то обучающий характер, так как на основе него проще понять общие принципы работы итерационных методов решения НАУ.

Итерационная формула метода простой итерации:

xn=ϕ(xn-1)

Скорость сходимости: зависит от ϕ(x)

Надежность сходимости: зависит от ϕ(x)

Метод Ньютона основан на уравнении касательной y=f’(x)*x+b, из которого в результате алгебраических преобразований выводится итерационная формула:

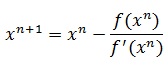
Плюсы метода:

  • Максимально высокая скорость сходимости, так как |ϕ’(x)|=0 во всех точках интервала локализации (здесь ϕ(x)-правая часть итерационной формулы);
  • Широкий спектр возможных начальных приближений (сравнительно с методом секущих). Главное, чтобы начальное приближение не попадало на отрезок, где функция монотонно возрастает или убывает и притом не пересекает ось абсцисс на исследуемом интервале локализации – это приведет либо к расходимости, либо к выходу итерационного процесса за пределы интервала локализации и приближению к корню соседнего интервала.

Минусы метода:

  • Наличие в итерационной формуле производной – производную не каждой функции можно определить;
  • Возникновение ошибки при выполнении f’(x)=0 – касательная параллельна оси абсцисс.

Геометрическая интерпретация:

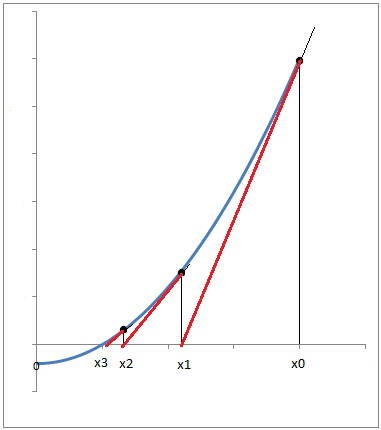
Скорость сходимости: высокая

Надежность сходимости: средняя

Существует несколько модификаций метода Ньютона, исключающие из итерационной формулы производную, но «жертвующие» другими характеристиками.

Например, для сравнительно простых функций производная вычисляется только однажды при первом приближении и в дальнейшем рассматривается как константа. В итоге страдает скорость сходимости, так как на последующих итерациях в точке соответствующей предыдущим приближениям проводится не касательная, а прямая параллельная касательной первой итерации. Итерационная формула в этом случае выглядит следующим образом:

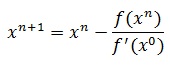
Одной из наилучших модификаций метода Ньютона считается метод секущих. Итерационная формула этого метода получается посредством замены производной в формуле Ньютона на приближенное значение. В итоге имеем:

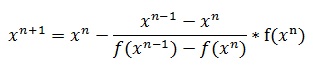
Из формулы очевидно, что данный метод двухшаговый, то есть для расчета текущего приближения необходимо наличие двух предыдущих.

Относительно метода Ньютона метод секущих ничуть не теряет в скорости, тем ни менее исключая все негативные моменты связанные с производной. Единственное, в чем он уступает своему прародителю, так это в том, что чуть больше становится ограничений на выбор начальных приближений – оба приближения должны быть расположены достаточно близко друг к другу и находиться на одном интервале убывания-возрастания с корнем уравнения. Этот метод также называют методом линейной интерполяции.

Геометрическая интерпретация:

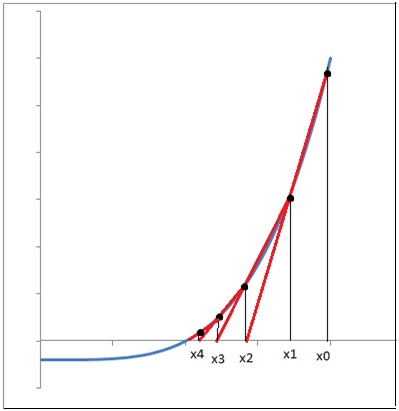
Скорость сходимости: высокая

Надежность сходимости: средняя

Гибридные алгоритмы

В последнее время широко применимы гибридные методы решения нелинейных уравнений, сочетающие в себе надежность и скорость. Примером такого гибрида является алгоритм ZEROIN, разработанный Деккером, а позже улучшенный Брентом. В этом методе соседствуют между собой методы бисекции, секущих и обратной квадратичной интерполяции.

В данной статье я представлю в виде программного кода некий прообраз ZEROIN’a, другими словами, урезанный ZEROIN. Я не стал включать в алгоритм метод квадратичной интерполяции, так как он только лишь ускоряет процесс решения, уменьшая количество итераций. Если коротко, то этот метод подобен методу секущих, только обладающий более высокой скоростью сходимости, за счет того что он интерполирует три точки, и, в результате, получается кривая, а не прямая как в методе секущих. Метод квадратичной интерполяции трехшаговый.

Как же работает этот гибрид? Я уже говорил, что метод секущих показывает отличные результаты на монотонных интервалах локализации корня. Дабы гарантировать эти монотонные интервалы, я исследую полученные локализацией подынтервалы на содержание точек перегибов, вводя условие f’(x)*f’(х+h)<=0. Если оно выполняется, то запускается метод бисекции, делящий отрезок пополам. То есть бисекция выполняется до тех пор пока не избавит интервал, на котором локализован корень от точек перегибов. Затем уже работает метод секущих до конца итерационного процесса. Вот и вся суть этого гибридного метода: бисекция обеспечивает надежность, а метод секущих скорость сходимости.

Но даже появление гибридных методов решения НАУ не исчерпывает ситуацию. В любом случае приходится анализировать функцию прежде чем употреблять численный метод, каким бы универсальным он не был.

Program Gibrid;

Const h=0.5; 

Var a,b,eps,c,x1,x2,x3:real; {a,b-границы исходного интервала}

i:integer;                   {eps-точность x1,x2,x3-приближения}

KeyUp:integer;               {keyUp-переменная с помощью, которой определяется}

IntArr:array of real;        {какой инт. лок. выбран}

                             {IntArr-дин.масс. в который записываются инт.лок.}

Function f(x:real):real; {искомая ф-ция}

  begin

  f:=x*x*x-x-0.2;

  end;

Function proizf(x:real):real; {ее производная}

  begin

  proizf:=3*x*x-1;

  end;

  

Procedure LokKorn(a:real;b:real); {локализация корней}

  var i:integer;

  begin

  i:=0;

  repeat

    begin

    if f(a)*f(a+h)<=0 then

      begin

      i:=i+1;

      Setlength(IntArr,i); {оператор Object Pascal, предназначенный для изменения}

      IntArr[i-1]:=a;      {размерности динамического массива. В Turbo Pascal не работает.}

      end;

    a:=a+h;

    end;

    Until a>b;

  end;



Procedure Bisek(a:real;b:real); {бисекция}

  begin

  c:=(b+a)/2;

  if f(b)*f(c)<=0 then x3:=c

  else x2:=c;

  end;

  

Procedure MetSek(a:real;b:real); {метод секущих}

  begin

  x1:=b-(a-b)/(f(a)-f(b))*f(b);

  end;

  

Begin

Writeln('Реализация гибридного алгоритма в PascalABC.Net');

Writeln('Введите нижнюю и верхнюю границы диапазона поиска корней уравнения');

Readln(a);

Readln(b);

LokKorn(a,b);

writeln('Выберите интервал локализации корня');

for i:=1 to length(IntArr) Do

  begin

  writeln('Чтобы выбрать интервал','(',IntArr[i-1],';',IntArr[i-1]+h,') нажмите ',i);

  end;

Readln(KeyUp);

for i:=1 To length(intArr) Do

  begin

  if KeyUp=i then 

    begin

    x3:=intArr[i-1];   {получение начальных приближений}

    x2:=IntArr[i-1]+h;

    end;

  end;

writeln('введите требуемую точность');

readln(eps); 

repeat

  begin

  if proizf(x3)*proizf(x2)<=0 then  {проверка условия на необходимость}

    begin                           {применения бисекции}

    Bisek(x3,x2);

    end

  else

    begin

    Metsek(x3,x2);

    x3:=x2;

    x2:=x1;

    end;

  end;

until Abs(x3-x2)<eps;

writeln(x2);

End.
Автор: Лебедев Максим
Дата публикации: 14.09.2010