Итерационные методы решения СЛАУ. Метод простых итераций. Метод Зейделя.

Содержание:

  1. Введение
  2. Метод простых итераций
  3. Метод Зейделя

Введение

Методы решения систем линейных алгебраических уравнений классифицируют на прямые (точные) и итерационные. Прямые методы основаны на выполнении конечного числа арифметических операций, это, например, метод обратной матрицы, метод Гаусса, метод Гаусса-Жордана, метод прогонки для трехдиагональных матриц и т.д. Суть итерационных методов, в свою очередь, заключаются в том, чтобы за счет последовательных приближений получить решение системы, определяемое необходимой точностью. Я попытаюсь наиболее подробно рассмотреть два из них, а именно метод простых итераций и метод Зейделя. Они практически эквивалентны, поэтому ограничусь подробным анализом метода простых итераций, а в конце пару слов скажу по поводу метода Зейделя. А прежде чем приступить к рассмотрению какого-то конкретного метода, хочется немного описать итерационные методы решения СЛАУ в общем плане.

Эти методы характеризуются большими расчетными объемами, что не мешает им быть по своей структуре достаточно простыми. Всего-навсего за счет предыдущих приближений мы получаем новые приближения, и, если система удовлетворяет условию сходимости, то эти приближения все меньше и меньше отличаются от аналитического решения.

Для итерационных методов можно выделить три последовательных этапа:

  1. Приведение исходной системы вида 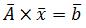к итерационной форме .
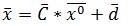  2. Проверка условия сходимости.
  3. Решение системы одним из методов.

Метод простых итераций


Теперь, опираясь на представленную последовательность, разберем метод простых итераций. Сразу условимся, что для общего вида систем выполняется тождество m=n, где m - количество уравнений в системе, n - количество неизвестных. Т.е. не имеет смысла решать недоопределенные (m<n) и переопределенные (m>n) системы, т.к. они могут быть сведены путем элементарных алгебраических преобразований к нормальным (m=n) системам линейных уравнений. Другими словами, если у вас имеется «ненормальная» система, то прежде, чем использовать метод простых итераций, преобразуйте ее к нормальной.

Все мы знаем, что система линейных уравнений может быть записана в матричной форме, где A – матрица коэффициентов, b – вектор свободных членов, x – вектор неизвестных. Возьмем систему:


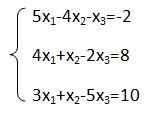
Ее матричная форма:


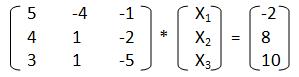
Смотрим на первый этап итерационных методов – он предполагает преобразование исходной системы, а именно матрицы А и вектора b к итерационной форме, где С и d – итерационные формы исходных данных.

Переход к итерационному виду осуществляется по следующим формулам:

cij = -aij/aii     di= bi/aii , где i, j = 1,2,3…

Также следует отметить, что, несмотря на эти формулы, диагональные элементы новой матрицы обнуляются, хотя должны быть равны -1.

В итоге для нашей системы должно получиться:


Проверьте. Ошибка? Если считать по исходной системе, то да. Все дело в том, что я не сказал про одно "НО".

Это "НО" заключается в следующем. Если мы будем преобразовывать исходную систему к итерационной форме, то она не удовлетворит условию сходимости:


Некоторые элементы матрицы C будут больше единицы. А глядя на условие сходимости, становится понятно, что, если хотя бы один будет больше единицы, то условие не выполнится, и решение системы путем простых итераций не будет найдено.

Поэтому открываем учебник по линейной алгебре и вспоминаем элементарные матричные преобразования! Прежде чем следовать этапам итерационных методов, нужно привести исходную систему к виду, в котором все диагональные элементы были бы максимальными по модулю в своих строках. Только при таком виде матрицы коэффициентов можно надеется на выполнение условия сходимости.

Смотрим нашу начальную систему. Видим, что третий элемент третьей строки по модулю больше других. Оставим его неизменным. Меняем местами первую и вторую строки. Теперь умножаем строку, ставшую первой, на -1 и складываем с новой второй. В итоге получаем:


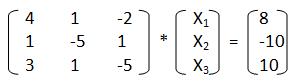
Теперь при подстановке в формулы мы получим итерационную форму верно. К сожалению, это преобразование начальной системы к "благоприятному" виду - чистая аналитика, поэтому записать его в программный код очень сложно, а если даже и попытаться, то в некоторых случаях вероятно возникновение ошибок.

Переходим ко второму этапу: "Проверка условия сходимости" (формулу смотрите выше). Если система не проходит проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. В этом случае можно попытаться получить другую "благоприятную" форму. Если условие сходимости выполнено, то стратегия метода простых итераций применима и осуществляется переход к третьему этапу.

В конечном счете, мы получили систему линейных алгебраических уравнений в итерационной форме:


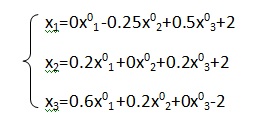
где x1, x2, x3 – приближения, получаемые на текущей итерации за счет приближений полученных на предыдущей итерации - x01, x02, x03.

Итерационный процесс в методе простых итераций идет до тех пор, пока вектор приближений не достигнет заданной точности, т.е. пока не выполнится условие выхода:

Max|xi-x0i|<ε, где ε – требуемая точность.

Я думаю, что теории достаточно, осталось лишь обратить внимание на программную реализацию метода.

Далее представлен код, написанный в среде PascalABC.Net. Эта система была выбрана мной благодаря возможности работать с динамическими массивами (в Turbo Pascal предусмотрены только статические). Поэтому программа может решать любую нормальную систему линейных уравнений, которая проходит проверку условия сходимости. Главное, чтобы вид этой системы соответствовал вышеописанным критериям.

Program MetodProstIter; {метод простых итераций}

Var

n:integer; {количество переменных или количество уравнений, как кому удобно - }

           {в любом случае они должны быть равны (m=n)}

A:array of array of real; {матрица коэффициентов}

b:array Of real; {вектор-столбец свободных членов}

C:array of Array of real; {матрица Якоби - итерационная форма матрицы А}

d:array of real; {итерационная форма вектора свободных членов}

Err:Boolean; {переменная, по значению которой после выполнения процедуры проверки}

             {сходимости определяется соответствие-несоответствие условию сходимости}

X:array of Real; {вектор неизвестных}



procedure InputA(var n:integer); {ввод матрицы А}

var

i,j:Integer;

begin

  SetLength(A,n); {именно эта встроенная процедура задает правую границу массива}

                  {в зависимоти от количества переменных}

  for i:=0 To n-1 Do

  begin

    SetLength(A[i],n); {многомерные массивы в PascalABC можно определять как массивы массивов}

  end;

  for i:=0 To n-1 Do

  begin

    for j:=0 To n-1 Do

    begin

      read(A[i,j]);

    end;

    writeln('');

  end;

end;





procedure InputB(var n:integer); {ввод вектора B}

var

i:Integer;

begin

SetLength(b,n);

for i:=0 To n-1 Do

begin

  readln(b[i]);

end;

end;





Procedure IterForm(A:array of Array of real;b:array of real;n:integer);

 {получение итерационной формы системы}

var i,j:Integer;

begin

  SetLength(C,n);

  for i:=0 To n-1 Do

  begin

    Setlength(C[i],n);

  end;

  SetLength(d,n);

  for i:=0 To n-1 Do

  begin

    for j:=0 To n-1 Do

    begin

      if i=j then

        C[i,j]:=0

      else

        C[i,j]:=-A[i,j]/A[i,i];

    end;

    d[i]:=b[i]/a[i,i];

  end;

end;





Procedure ProverkaShodimosti(C:array of array of real;d:array of real;n:integer);

 {проверка системы на сходимость}

var i,j:Integer;

summ:real;

begin

  summ:=0;

  for i:=0 To n-1 Do

  begin

    for j:=0 To n-1 Do

    begin

      summ:=summ+C[i,j]*C[i,j];

    end;

  end;

  if SQRT(Abs(summ))>1 then

  begin

    writeln('Данная система не удовлетворяет условию сходимости');

    Err:=True;

  end

  Else Err:=False;

end;





Procedure ProstIterMetode(C:array of array of real;d:array of real;n:integer);

 {cобственно, сама стратегия метода простых итераций}

var i,j:Integer;

X0:array of real;

delta:real;

E:array of real;

begin

  SetLength(X0,n);

  SetLength(X,n);

  Setlength(E,n);

  X0:=Copy(d);

  repeat

  begin

    for i:=0 To n-1 Do

    begin

      X[i]:=0;

      for j:=0 To n-1 Do

      begin

        X[i]:=X[i]+C[i,j]*X0[j];

      end;

      X[i]:=X[i]+d[i];

      E[i]:=Abs(X[i]-X0[i]);

    end;

    delta:=E[0];

    for i:=1 To n-1 Do

    begin

      if delta<E[i] then delta:=E[i];

    end;

    X0:=Copy(X);

    end;

  Until delta<=0.000001; 

  writeln('решение системы равно вектору:');

  For i:=0 To n-1 Do

  begin

    Writeln(X[i]);

  end;

end;



BEGIN

Err:=False;

writeln('Введите количество переменных');

Readln(n);

writeln('Введите матрицу коэффициентов');

InputA(n);

writeln('введите матрицу свободных членов');

InputB(n);  

IterForm(A,b,n);

ProverkaShodimosti(C,d,n);

if Err=False then ProstIterMetode(C,d,n);





END.

Применимо к нашей СЛАУ программа выдаст ответ: x1=1.0000002, x2=2.000000009, x3=-1.0000002. Такой вектор приближений соответствует точности 10-6, прописанной в коде.


Метод Зейделя


Как я уже говорил, метод простых итераций и метод Зейделя почти идентичны. Разница лишь в том, что в методе Зейделя расчет вектора приближений на текущей итерации происходит с использованием данных, полученных ни только на предыдущей, но и на нынешней итерации. То есть элемент x1 вычисляется на основе x2 и x3, значения которых, расчитаны на предыдущей итерации, а следующий элемент x2 уже вычисляется за счет x1, полученного именно на текущей итерации, и x3 на предыдущей. Другими словами данные в методе Зейделя для расчета вектора X поступают в процесс по мере их вычисления. А в методе простых итераций используются данные, строго полученные на предыдущей итерации.

Это различие говорит нам о том, что метод Зейделя обладает наилучшей сходимостью нежели метод простых итераций, так как для него характерна тенденция использования приближений, получаемых по ходу процесса, наиболее близких к конечному результату.

И на последок покажем это различие в практической реализации. Чтобы метод простых итераций "превратился" в метод Зейделя нужно поменять процедуру ProstIterMetode, например, на следующую:

Procedure Zeidel(C:array of array of real;d:array of real;n:integer); 

var i,j:Integer;

X0:array of real;

delta:real;

E:array of real;

promX:array of real;

begin

  SetLength(X0,n);

  SetLength(X,n);

  Setlength(E,n);

  Setlength(promX,n);

  X0:=Copy(d);

  promX:=Copy(d);

  X:=Copy(d);

  repeat

  begin

    for i:=0 To n-1 Do

    begin

      X[i]:=0;

      for j:=0 To n-1 Do

      begin

        X[i]:=X[i]+C[i,j]*promX[j];

      end;

      X[i]:=X[i]+d[i];

      promX:=Copy(X);

      E[i]:=Abs(X[i]-X0[i]);

    end;

    delta:=E[0];

    for i:=1 To n-1 Do

    begin

      if delta<E[i] then delta:=E[i];

    end;

    X0:=Copy(X);

    end;

  Until delta<=0.000001; 

  writeln('решение системы равно вектору:');

  For i:=0 To n-1 Do

  begin

    Writeln(X[i]);

  end;

end;
Автор: Лебедев Максим
Дата публикации: 20.07.2010