Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.
Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.
program mdp;
function f(x: real): real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
var
a, b, eps, x: real;
BEGIN
write ('Левая граница интервала:'); readln(a);
write ('Правая граница интервала:'); readln(b);
write ('Точность:'); readln(eps);
while abs(b-a)>eps do
begin
x:=(a+b)/2;
if f(a)*f(x)<0 then b:=x else a:=x;
end;
writeln ('x=',x:3:3,' f(x)=',f(x):4:4);
readln();
END.
Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.
program mdp;
function f(x: real): real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
var
a, b, eps, x: real;
BEGIN
write ('Левая граница интервала:'); readln(a);
write ('Правая граница интервала:'); readln(b);
write ('Точность:'); readln(eps);
repeat
x:=(a+b)/2;
if f(a)*f(x)<0 then b:=x
else a:=x;
until abs(f(x))<eps;
writeln ('x=',x:3:3,' f(x)=',f(x):4:4);
readln();
END.
Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:
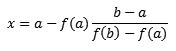
После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.
Program Hord;
function f(x: real): real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
var
a, b, eps, x: real;
BEGIN
write ('Левая граница интервала:'); readln(a);
write ('Правая граница интервала:'); readln(b);
write ('Точность:'); readln(eps);
Repeat
x:=a-f(a)*(b-a)/(f(b)-f(a));
if f(a)*f(x)<=0 then b:=x
else a:=x;
Until abs(f(x))<=eps;
writeln ('x=',x:3:3,' f(x)=',f(x):4:4);
readln();
END.
Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.
В основе метода Ньютона лежит разложения функции в ряд Тейлора:
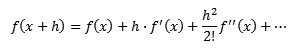
Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.
Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:
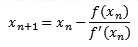
Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом
Program Newton;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Function f1(x:real):real;
begin
{Здесь приводим выражение для производной функции }
f1:=3*x*x+2*x+1;
end;
var
eps, x: real;
BEGIN
write ('Начальное приближение:'); readln(x);
write ('Точность:'); readln(eps);
Repeat
x:=x- f(x)/f1(x);
Until abs(f(x))<=eps;
writeln ('x=',x:3:3,' f(x)=',f(x):4:4);
readln();
END.
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.
Дата публикации: 05.03.2010